乒乓球有多复杂,我们以数字建模的方式来说明,先假设乒乓球只有不转球,而且回球路线只有直线,而且每次都回到对方右边底线,设定这种情况为1。

道法有云,一生二,二生三,三生万物。有了这个1,就会有无数种千变万化的情况。
还是不转球,回球路线还是直线,但落点大致有三处,右边小三角、球台中部右侧、右边大角,1*3=3,变为3种情况。
回球路线有直线、中路、斜线,3*3=9。
球又有不转、上旋、下旋、侧上旋、侧下旋,9*5=45
这一下头开始大了,如果把半边球台看作是九宫格,发球第一落点又大致有9种情况,45*9=405。
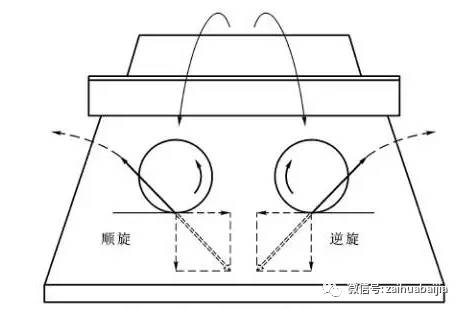
而每一种旋转又大致分3种情况,不转、稍转、巨转,这只是大致的分法,细分的话,数字大得吓人。上旋、下旋、侧上旋、侧下旋分别乘以3,等于12种,405*12=4860。
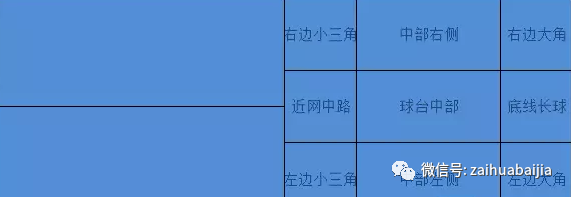
按照粗略的分法,就将近2万种变化,如果分得再细一点,那还了得?
所以打球时,大脑高速运转,人不聪明才怪呢!
想健康吗?来打乒乓球吧!
想聪明吗?来打乒乓球吧!
